The cost paradox: Why a better cost calculation, may reduce profits

By Pascal Pollet – Sirris, Belgium
The pricing of a product has a large influence on the sales revenue and the profit. Surprisingly, research shows that a more accurate cost estimation does not automatically lead to a higher profit.
Two methods are commonly used to determine the price of an industrial product. One method is to align the price with the known market prices, another way is to estimate the cost and to add a profit margin. This last ‘cost-plus’ method is the most popular in the industry. Many industrial products are custom made, which means that the competitor’s price is not publicly known anyway.
Uncertainties in pricing
The price is highly dependent on the cost calculation when using cost-plus pricing. In practice, it is often not easy to estimate in advance what the cost will be. Comparisons based on the registered production times typically show deviations between the actual and estimated production times. The material prices actually paid and the material consumption can also deviate from the previously estimated material costs.
Determining the profit margin is even more difficult. The margin often depends on all kinds of market circumstances: who are the alleged competitors, what is the price sensitivity of the customer, to what extent does the salesman experience pressure to achieve his sales targets.
Due to these uncertainties, it is possible that for similar price requests a low price may be quoted in one case, and a higher price at another instance. Of course, competitors also experience similar uncertainties, which means that their prices will also be spread out.
By opting for the lowest-priced offer, the customer will be able to benefit from this price spread. At first sight, the customer seems to be the winner in this game and the supplier the loser. “Orders for which we have underestimated the cost are ordered, while the offers for which we have correctly estimated the cost are lost to the competitor”, is therefore an often heard saying in the industry.
Intuitively, one would think that improving the cost calculation is the solution. The more accurately we know the cost, the better we can set the price, and the more profitable the company can become. Sounds logical, but is this really true? Does a better cost estimation really lead to a higher profit?
Impact on the quotation success rate
Let’s set up a thought experiment to find out what the influence of the price spread is on a company’s profits. For this purpose, we assume for a moment that a customer requests a quotation from 3 companies (A, B, and C). In order to map out the impact of the price spread, we will assume that the three suppliers are otherwise similar. The products and services of the three competitors are similar, so the choice of the customer depends entirely on the pricing. In addition, the three competitors have a similar cost structure so that the average price offered is the same. The price differences between the three companies are therefore only due to the uncertainties mentioned above.
In our example, we will assume that the price may vary by +/- 10% for all companies due to the uncertainties. In our example, we will assume an average price of 100 euro, so the lowest quoted price is 90 euro, and the highest quoted price is 110 euro.
Since the three companies are similar in all respects, they each have the same probability to offer the lowest price and thus win the order. The success rate of an offer is therefore one third (33.3%). However, company A is dissatisfied with the current state of affairs and devises a better cost calculation method that eliminates the uncertainties. This method reduces the price spread to zero resulting in a constant price of 100 euros.
What is now the success rate of a quotation? If company A wants to win the order, its price must be the lowest, which means that the price of competitor B and C must be somewhere in the higher price range of 100-110 Euros. The probability that the price of company B is in this upper half of the price range is 50%. The same holds for company C. The probability that both competitors are in this higher price range is thus 50% x 50% = 25%. The success rate of a quotation and thus the market share of company A will therefore drop from 33.3% to 25% when company A perfects its cost calculation!
But what if company A would have acted the other way around and had spent less energy on its cost estimation resulting in less accurate quotations? To answer this question, we show in figure 1 the impact of company A’s price spread on the success rate of quotations. The horizontal axis shows the relative price spread. The relative price spread is the ratio of company A’s own price spread to the price spread of the competitors. With a relative price spread of 1, all companies have the same price spread and the success rate is 33.3%. With a relative price spread of zero, there is no longer a spread on the price of company A and the success rate becomes 25%, while with a price spread of two, the spread on the prices of A is twice as large as that of the competitors. In this case we see the success rate of the quotations climb to more than 40%.
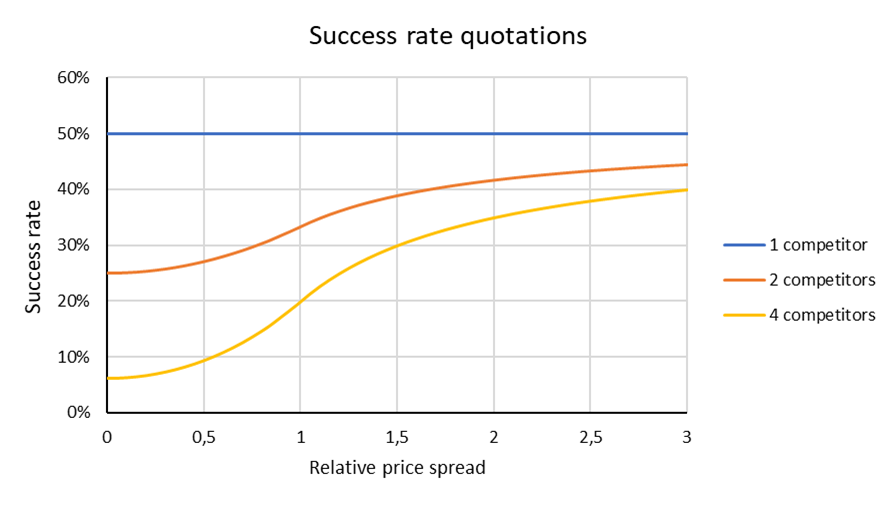
Figure 1: Impact on the success rate of quotations of the relative price spread and the number of competitors (calculated with a uniform distribution of prices).
The figure also shows the impact of the number of competitors of company A. If the customer only requests a quotation from two companies, the success rate is always 50% and no longer depends on the relative price spread. The more quotations a customer would request, the greater the decrease in the success rate becomes when refining the price calculation. For example, if company A faces 4 competitors for an offer, the success rate decreases from 20% (= one in five) to 6.25% (= 50% x 50% x 50% x 50%). Note that in our context, the number of competitors for company A is determined by the number of quotes the customer requests, not by the total number of competitors of company A in the market.
Impact on revenue
The above picture shows the success rate of the quotations, and therefore the market share (in units sold). If the price spread increases, the success rate increases, but this is because more quotations with a lower price are sent out. The question therefore arises as to the impact of the price spread on the revenue, and ultimately on the profits.
Let’s first look at the revenue. To estimate the impact of the price spread on revenue, we made some calculations which are depicted in Figure 2.

Figure 2: Impact on the average revenue per quotation as a function of the relative price spread and the number of competitors (calculated for an average price of 100 Euro and a uniform price spread of the market of +/- 10%).
The calculations and the figure 2 provide us with the following insights:
• If the customer requests only two offers (company A has one competitor), then the revenue could increase slightly by 3.5% when the calculation is perfect. In practice, this impact will be much smaller because such perfect calculations are not possible.
• If the customer requests a quote from three companies (company A has two competitors), then the revenue will decrease by 21% when the calculation is perfect. As with the success rate, this decrease is even more pronounced when the customer requests even more quotes.
• If the price setting becomes less accurate than the price setting in the market (relative price spread greater than one), the revenue first increases, after which it reaches a maximum, and then slowly decreases again. In our example with two competitors, the maximum is reached at a price spread of +/-25% (a relative price spread of 2.5 compared with the competitor price spread of +/- 10%.)
Impact on profitability
Now that we know the impact on the quotation success rate and the revenue, we are able to calculate the impact on the profitability. Here, we have to take into account the effect on the variable costs and the fixed costs. The total variable cost (e.g. material cost) is determined by the production volume and is therefore proportional to the success rate of the quotations. The fixed cost is – within certain limits – independent of the production volume and is not influenced by the price setting.
Hence, it is sufficient to calculate the difference between revenue and the total variable cost to understand the impact of the price uncertainties on the profit. This difference is called the contribution. The higher the contribution, the higher the profit.
A special case occurs when the customer only requests two quotations. In this case, the success rate is no longer dependent on the price spread and is always 50%. As a result, the production volume and therefore the total variable cost are constant. This implies that the contribution and the profit will only depend on the revenue. Hence, the profit will behave as the revenue and will show a slight increase when improving the cost estimation.
Figure 3 shows the results of our calculations when the client requests three quotations (our company A has 2 competitors) for different variable costs: 60%, 80%, 90% of the average price.

Figure 3: Impact on the average contribution per requested quotation as a function of the relative price spread with 2 competitors (calculated for an average price of 100 euros and a uniform price spread in the market of +/- 10%).
From figure 3 and the underlying mathematics, we can once again draw some surprising conclusions:
• The behavior of the contribution and the profit depends on the share of the variable costs. If the share of the variable cost compared to the average price is very high, improving the cost calculation will increase the profit.
• If the share of the variable cost is relatively low, improving the cost estimation will cause the profit to decrease. In this case it is even advisable to spend less energy on the quotation process and come up with a less accurate cost estimate. In the example with a variable cost of 60% of the average price, the profit reaches a maximum when the uncertainty of the price calculation goes up from +/- 10% to +/- 15%.
• At a certain share of the variable cost, improving the cost estimating has no effect, but the profit will deteriorate if you make the cost estimation less accurate. In our example, this tipping point lies at a variable cost of 80 Euro (80% of the average price), or equivalent with a contribution of 20 Euro per product. Note that the contribution of 20 Euro neatly corresponds to the price range in the market (difference between highest and lowest price: 110-90 = 20 Euro). This is no coincidence. In general, as a rule of thumb, the tipping point in the case with 2 competitors for an offer occurs when the contribution of a product is roughly equal to the price range of the market.
So, if the contribution of an order is greater than the price spread in the market, improving the cost calculation will reduce profits. In practice, this will often be the case. This observation brings us to the cost paradox: “Knowing your costs better, may lead to lower profits!”
Practical implications
The cost estimation process is often judged by its accuracy through comparing the estimated costs with the actual registered costs. This has two important consequences.
First, the focus on cost accuracy can trigger a blame game between the management and the production workers. Was too much time spent because of a miscalculation, or because of substandard work by the production staff?
Secondly, cost calculators will spend an excessive amount of time to make their cost estimate as accurate as possible to avoid blaming. As a result, they will overload themselves and the customer will have to wait a long time for a quote.
As many customers highly value short quotation times, it is often better to aim for speed in the quotation process than for accuracy. A fast quotation process will often lead to a higher success rate on its own, and as explained earlier, the potential inaccuracies might not be as damaging as your intuition would lead you to think.
Find out more about QRM and what it can do for your company
